A comparison of Peg-Thing written in Clojure, Python and functional Python
2019-08-19
Intro
Currently, I am learning Clojure reading the great (and free) book Clojure for the brave and true. In chapter 5, the game Peg-Thing is implemented. I thought this would be a good opportunity to compare Python and Clojure. I reimplemented the game in Python two times. First in the 'normal' Python way and a second time in a way that seemed to me like the ideal functional implementation in Python.
Peg-Thing
Peg-Thing, for those that don't know, is a single player board game. The board has a triangular shape, is missing one peg in the beginning. The following images were ruthlessly stolen from the aforementioned book:
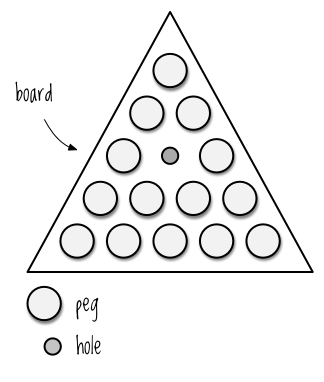
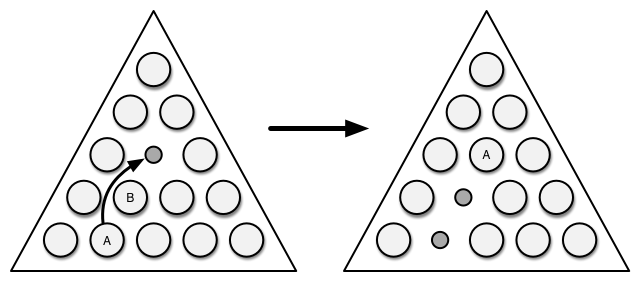
To make a move, you take one peg and move it over another peg to a free position, and remove the peg that was passed over:
The goal is to remove as many pegs as possible before the board reaches a state without valid moves, in which case the game is over.
Triangular numbers
All implementations utilize the series of triangular numbers, which is defined as follows:
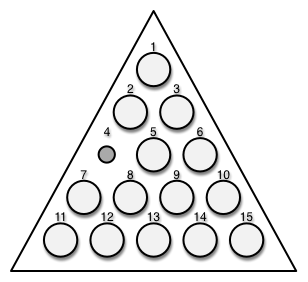
So the series begins with 1, 3, 6, 10, 15, .... These numbers represent the
number of the last field in the nth row of a triangle:
A Clojure crash course
Before we start looking at Clojure code, I will provide a little crash course on how to read it.
In Clojure, a function call is written as a list where the first element is the
function name and the remaining elements are its arguments. For example, calling
a function named foo without arguments would look like this: foo() in Python
and like this: (foo) in Clojure. This is the only way to invoke a function in
Clojure, therefore foo(x + 1) would be (foo (+ x 1)) in Clojure. But
actually a clojure programmer would much rather write (foo (inc x)) as inc
is short for "increment" and returns one plus its argument.
Functions are defined via defn like this:
(defn <function-name> [<args>]
<Body>)
Functions can be overloaded in which case a function definition looks like this:
(defn <function-name>
([<args1>] <Body1>)
([<args2>] <Body2>))
Anonymous functions can be defined via fn like this: (fn [<args>] <Body>)
and can be overloaded too. A shortcut to define an anonymous function is
#(<Body>). In the second version the %-sign can be used to refer to the
argument if it is the only one or %<n> for the nth argument if there are
more.
To assign a value to a symbol in the global namespace you can use def e.g.
(def my-val 1) or (def my-func (fn [] (println "Hello"))). def always
creates a symbol in the global scope, even if called from within a function. To
create a local variable let is used like this:
(let [<name1> <value1>
<name-n> <value-n>]
<Body>)
The symbols defined by let are only valid within its body.
Into the code
When I first started writing this article I wanted to present every version one
by one and then compare them afterwards. I had to realize that this would make
one very long article and therefore decided to directly compare interesting
code snippets. You can download the code for all versions here. For
convenience, I packed together some functional utility functions from other
libraries with Toolz and added some aliases and imports I commonly use. Now I
can use from toolzEx import * and have everything at my fingertips and it's
used in the functional Python version. In case you want to run them yourself,
you can find it here.
Generating the triangular numbers
First, we need to generate the triangular numbers. In Clojure it's done like this:
(defn tri*
([] (tri* 0 1))
([c-sum n]
(let [new-sum (+ c-sum n)]
(cons new-sum (lazy-seq (tri* new-sum (inc n))))))
The first line says "define a function named tri*" (Clojure is very generous
with allowed characters in symbol names). This function has two versions: one
without arguments, which is defined in the second line, and one with two
arguments which is defined from the third line on. The first version does
nothing but calling the second version with the arguments 0 and 1.
The second version is a little mind-bending - first, I'll quickly explain the
elements it consists of:
- cons is a function that prepends an element to a sequence
- lazy-seq evaluates a sequence, but only after an element was requested. Also, it stores generated elements.
So calling tri* without arguments will return a lazy sequence which contains
the already computed value for the first element and the recipe to compute
the rest.
This sequence is then stored with the name tri like this:
(def tri (tri*))
Then, there are a few utility functions to work with the sequence. I am not going to explain them in depth (if you are interested in that, you can find more details in the book ), but the comments will explain what they do:
; Check whether n is triangular
(defn triangular? [n]
(= n (last (take-while #(<= % n) tri))))
; Get the nth triangular number, i.e. the number of the nth row.
(defn row-tri [n]
(last (take n tri)))
; Find the row of pos by checking the index of the first tri-num
; that is greater than pos
(defn row-num [pos]
(inc (count (take-while #(> pos %) tri))))
This has a certain elegance to it as at any time any number can be requested and only the minimally required amount of computation will take place.
In Python, we could use a generator for this:
def tri_num_gen():
acc = 0
n = 1
while True:
yield acc
acc += n
n += 1
tri_nums = [tri for tri, i in zip(tri_num_gen(), range(26))
def row_num(x):
return next(i for i, tri in enumerate(tri_nums)
if tri >= x)
This approach is much more blunt. We simply generate the first 26 numbers and
hope that they will suffice. On the other hand it has some advantages. We don't
need to define a function to check whether n is a triangular number as we can
use n in tri_nums and we don't need an equivalent for row-tri because we can
use tri_nums[n].
The only thing that differs in the functional Python version is:
tri_nums = ltake(26, tri_num_gen())
def row_num(x):
return first(i for i, tri in enumerate(tri_nums)
if tri >= x)
take and first are from Toolz,
and ltake(...) is short for list(take(...)). I think this version is
a little nicer to read, but it's basically the same.
The board representation
The Clojure community follows the motto "it is better to have 100 functions operate on one data structure than 10 functions on 10 data structures". And consequently the Clojure implementation uses nested maps (or dicts in Python lingo) to represent the board. The data structure looks like this:
{1 {:pegged true, :connections {6 3, 4 2}},
2 {:pegged true, :connections {9 5, 7 4}},
3 {:pegged true, :connections {10 6, 8 5}},
4 {:pegged true, :connections {13 8, 11 7, 6 5, 1 2}},
5 {:pegged true, :connections {14 9, 12 8}},
6 {:pegged true, :connections {15 10, 13 9, 4 5, 1 3}},
7 {:pegged true, :connections {9 8, 2 4}},
8 {:pegged true, :connections {10 9, 3 5}},
9 {:pegged true, :connections {7 8, 2 5}},
10 {:pegged true, :connections {8 9, 3 6}},
11 {:pegged true, :connections {13 12, 4 7}},
12 {:pegged true, :connections {14 13, 5 8}},
13 {:pegged true, :connections {15 14, 11 12, 6 9, 4 8}},
14 {:pegged true, :connections {12 13, 5 9}},
15 {:pegged true, :connections {13 14, 6 10}},
:rows 5}
as opposed to Python, no colon is needed between keys and values. Also, commas are not required to separate key value pairs, but can be used since they are treated as white space. Just imagine the words starting with a colon were strings. In this map, the positions are used as keys. For every position, we store whether it is pegged, and the target fields that you can jump to together with the fields you jump over to get there. For example: from field 1 you can jump to 6 by hopping over 3 and to 4 by hopping over 2.
But we don't define the board statically. We compute it by the number of rows it should have:
(defn new-board [rows]
(let [max-pos (row-tri rows)]
(reduce (fn [board pos] (add-pos board max-pos pos))
{:rows rows}
(range 1 (inc max-pos)))))
it reduces the possible positions over add-pos with {:rows rows} as initial
value. In case you don't know how reduce works, you can find an explanation
here.
Then add-pos will add all valid connections:
(defn add-pos [board max-pos pos]
(-> (assoc-in board [pos :pegged] true)
(connect-right max-pos pos)
(connect-down-left max-pos pos)
(connect-down-right max-pos pos)))
assoc-in will return a new map where the key-path [pos :pegged] is set to
true. The -> macro will then take the output of that and provide it as
leftmost input to the connect-right function. So the line with connect-right
becomes (connect-right (assoc-in board [pos :pegged] true) max-pos pos),
the result of that passes as leftmost argument to
connect-down-left and the result of that to connect-down-right. The last
result will then be returned. The connection functions will always create two
connections, the one they are named after, and the inverse one. I think this is
a pretty elegant approach as it defines a pipeline of computations that the
initial board "flows" through.
The three connect functions are all pretty similar and I will only show you one of them:
(defn connect-down-left [board max-pos pos]
(let [row (row-num pos)
neighbor (+ row pos)
destination (+ 1 row neighbor)]
(connect board max-pos pos neighbor destination)))
First, row is defined and then used to get the left down neighbor (in row n,
you have to add exactly n to get there) and then this is repeated to get the
destination. Finally connect is called to create the connection.
connect looks like this:
(defn connect [board max-pos from over to]
(if (> to max-pos)
board
(reduce (fn [nb [from to]]
(assoc-in nb [from :connections to] over))
board
[[from to] [to from]])))
If to (the destination) is greater than max-pos it would not be on the
board, therefore nothing is done, and the original board is returned. This way
invalid connections are ignored. The anonymous function that is used in reduce
will simply add a the connection, first with the connection ([from to]) then
with the inverse connection ([to from]).
The normal Python version
In this version, I implemented the board as a class that has a list of fields. A field is a class itself, containing a variable to note whether it is pegged, its own id and a list of possible connections which are named tuples:
Connection = namedtuple('Connection', 'start, to, by')
@dataclass
class Field:
id: int
pegged: bool
connections: List[Connection]
class Board:
def __init__(self, rows):
self.fields = [Field(i, True, []) for i in range(tri_nums[rows] + 1)]
self.rows = rows
self.score = 0
for f in self.fields:
Board._connect(f, self.right_of)
Board._connect(f, self.down_left_of)
Board._connect(f, self.down_right_of)
In vanilla Python, one would use a mutable object here, so I first created the
board with all its fields and then added the connections via the static method
_connect, which looks like this:
@staticmethod
def _connect(field, next_field):
n = next_field(field)
nn = next_field(n) if n else None
if n and nn:
field.connections.append(Connection(field, nn, n))
nn.connections.append(Connection(nn, field, n))
This time, the targets of the connections are no integers but the actual field
objects. One of the next_field methods looks like this:
def right_of(self, field):
if field.id not in tri_nums:
return save_get(self.fields, field.id + 1)
The nice thing about this is that it is much easier to understand than the clojure version. Another advantage will become apparent when we take a look at the other methods. Nevertheless this is mutable, and I really have developed a strong appreciation for immutability which tends to prevent a lot of nasty bugs.
The functional Python version
Actually, I implemented this version twice, the first time mimicking the clojure implementation, but found that I prefer object notation, which I find easier to read, so I did it a second time, which is the version I'll show here, though I did include the first one in the zip.
I wanted something closer to the vanilla Python version. For that I used
the library Pyrsistent. It provides immutable equivalents for the standard
data structures as well as means to create immutable classes. I used
their PRecord class which allows to make a class that is basically an
immutable dict with key access like a namedtuple:
Connection = namedtuple('Connection', 'start, end, by')
class Position(PRecord):
pegged = field(bool, initial=True)
connections = pvector_field(Connection)
class Board(PRecord):
rows = field(int)
positions = pmap_field(int, Position)
So far this looks pretty similar to the vanilla version, the difference becomes
apparent if we look at the initialization which I moved to a static method as I
didn't want to mess with the default __init__. A notable difference is that
here a pmap is used to store the fields.
@curry
def connections(max_pos, dir_func, pos):
by = dir_func(pos)
end = dir_func(by) if by else None
return [Connection(pos, end, by),
Connection(end, pos, by)]\
if end is not None and end <= max_pos else [None]
class Board(PRecord):
rows = field(int)
positions = pmap_field(int, Position
@staticmethod
def new(rows):
cs = connections(tri_nums[rows])
con_map = thread_last(range(1, tri_nums[rows] + 1),
(mapcat, juxt(cs(right), cs(down_right), cs(down_left))),
concat,
(filter, bool),
(groupby, X.start))
return Board(rows=rows, positions=pmap(
valmap(lambda cons: Position(connections=pvector(cons)),
con_map)))
This code is a little harder to read again. I guess that's natural as going for
immutability is a restriction. Let's look at the new method.
thread_last is the same as Clojure's -> macro
except for the fact that the result from one call is provided as the last argument
to the next call (which makes it completely identical to Clojure's ->>).
The logic here is as follows: We can't create the fields first and add the
connections afterwards as the fields are immutable, so we have to add the
connections to the fields when they are created. Therefore the connections are
generated first by the connections function. It is curried which means that
calling it with incomplete parameters will return the function with the provided
parameters already set (i.e.
connections(x, y, z) == connections(x)(y,z) == connections(x)(y)(z)).
juxt returns a function that applies all provided functions (the three connect
versions) to its parameter, and returns the results in a list. mapcat is a
normal map with a concatenate afterwards, so instead of a list of lists of lists
of connections only a list of lists of connections will be returned.
This is then concatenated again, so that we are left with a list of connections
and Nones for those cases where the requested connection was invalid. These are
then filtered out in the next step, where every entry in the list that evaluates
to False (i.e. the Nones) will be filtered out. The X in X.start is just a
rename of fn's underscore, and returns a
function that accesses the start attribute of its argument. Consequently the
list of connections is transformed into a dict where all connections that start
from the same positions are found under that position as key.
This dict is then transformed into a dict with the same keys where the values are
Position objects (by valmap), which is then assigned to the Board that is
returned by the new method.
For completeness, this is the right function:
def right(pos):
return pos + 1 if not pos in tri_nums else None
Finding valid moves
In Clojure the valid-move? function looks like this:
(defn valid-move? [board from to]
(get (valid-moves board from) to))
It queries all valid moves for the position where move starts, and tries to get
the key with the target position from the resulting dict. If the key exists, an
integer is returned, which evaluates to true (in clojure everything
evaluates to true except for nil and false). valid-moves looks like
this:
(defn valid-moves [board pos]
(into {}
(filter (fn [[destination jumped]]
(and (not (pegged? board destination))
(pegged? board jumped)))
(get-in board [pos :connections]))))
The point where the computation starts is (get-in board [pos :connections])
which returns the connection map for the given position. In Clojure, iterating a
dict will automatically yield the key value pairs (like dict.items in Python).
These pairs are then filtered by checking whether the destination position is
unpegged and the jumped position is pegged. The results are then integrated into
a map again with into. pegged? is defined as follows:
(defn pegged? [board pos] (get-in board [pos :pegged]))
Logic-wise I really like this implementation, but having to start to read at the
bottom of a valid-moves feels a little strange. That might be due to lacking
familiarity though.
The normal Python version
This version is pretty straightforward:
def valid_connection(self, start, to):
connections = [c for c in self.fields[start].connections
if c.to.id == to]
if len(connections) == 0:
return False
c = connections[0]
if c.start.pegged and c.by.pegged and (not c.to.pegged):
return c
This is where we can really profit of the object notation, it allows for easy and very readable handling of board logic.
The functional Python version
The structure of the programs is not completely identical as I wrote them with multiple day gaps, in the functional version the function looks like this:
def find_connection(self, start, end):
try:
con = first(con for con in self(start).connections
if con.end == end)
if self(con.start).pegged and self(con.by).pegged \
and not self(con.end).pegged:
return con
except StopIteration:
return None
I added a __call__ method to the class to directly access the fields by index.
I think this is easy to read as well as elegant. Of course it could have been
done like this in vanilla Python too, if the first was replaced by a next.
The main difference is how we access the pegged fields. I like the vanilla
version in that regard much more, and I thought about how to do this in
this version for quite a while until I realized it is not possible. In the
vanilla version there is a reference circle, which can only be created if you
can manipulate an object after its creation. While I liked the notation for the
pegged checks that it enables, this is a typical scenario where a more complex
app could have some nasty bugs. And making this mistake is impossible by using
functional idioms. Yay!
Making a move
In clojure, applying a move to the board looks like this:
(defn make-move [board from to]
(if-let [jumped-pos ( valid-move? board from to )]
(-> (remove-peg board jumped-pos)
(move-peg from to))))
If the move is valid, the jumped peg is removed, and the jumping peg is moved.
This represents the game logic quite well.
Here are move-peg and remove-peg:
(defn remove-peg [board pos] (assoc-in board [pos :pegged] false))
(defn place-peg [board pos] (assoc-in board [pos :pegged] true))
(defn move-peg [board from to] (place-peg (remove-peg board from) to))
In the Python version I made sure that only valid moves would be passed to this function, therefore there is no check for validity here.
def update(self, move):
move.start.pegged = False
move.by.pegged = False
move.to.pegged = True
self.score += 1
move is a connection object as returned by valid_connection. And we can profit
again from that pesky mutability.
The functional version looks like this:
def make_move(self, start, end, by):
return self.toggle(start).toggle(end).toggle(by)
I like this version the most by far. Each toggle returns a new version of the board,
with the applied change, so we can chain the operations with a dot. It is easy
to read and immutable, jackpot! Here is the toggle method:
def toggle(self, pos):
return self.transform(['positions', pos, 'pegged'], op.not_)
transform is defined by PRecord and as assoc-in takes a 'path' to the value.
Unlike assoc-in it takes a function by which the value is changed instead of
taking a new value.
The main logic
In clojure the main logic is distributed along the IO-functions:
prompt-rows asks for how many rows the board should have, then creates
the board and calls prompt-empty-peg which asks which peg to remove, and
removes it. prompt-empty-peg then calls prompt-move to ask the player for
a move. Depending on whether the move was valid or not prompt-move will call
user-entered-invalid-move, or prompt-move again, or possibly game-over.
This is a lot of boring IO-code, and I will not show it here. I don't like this
design as it could (even in clojure) blow up the stack if someone decides to
play enough rounds (which is in the millions and completely unrealistic, but
still).
The normal python version looks like this:
def main():
size = query_size()
board = Board(size)
start_pos = query_valid_start_pos(board)
board.remove_peg(start_pos)
while board.valid_move_exists():
print('This is your board:')
print(board)
move = query_valid_move(board)
board.update(move)
print('This is your final board state:')
print(board)
print('You removed', board.score, 'pegs')
and the functional Python version looks like that:
@trampoline
def play(board):
if not board.valid_move_exists():
return board
print('\nThis is your board:')
print(board)
move = query_valid_move(board)
return R(board.make_move(*move))
def main():
size = query_size()
init_board = Board.new(size)
print(init_board)
start_pos = query_valid_start_pos(init_board)
final_board = play(init_board.toggle(start_pos))
print('This is your final board state:')
print(final_board)
print('You removed', final_board.missing_pegs() - 1, 'pegs')
To avoid mutability I replaced the while loop with a recursive function, the
trampoline is stolen from fn and allows the use of recursion without
blowing up the stack. Returning R means "call me again, and use these
parameters".
Conclusion
It's safe to say that the mutable python code is the easiest to read, while the clojure code is the hardest (at least for a Python programmer). Using functional idioms in python is comfortably possible, and makes it easier to avoid bugs by using libraries like Toolz, Fn and Pyrsistent. In Python the functional versions will run a little slower but in most scenarios that does not matter, Clojure on the other hand will probably run faster (I didn't run any benchmarks). In terms of size they are all pretty similar: the clojure file has 142 lines, the vanilla version 121 and the functional version has 124. That being said, I've put way more effort into the functional version than into the vanilla one, and it could certainly be shorter. The same goes for the clojure version, which I assume was optimized by the author of Clojure for the brave and true to be understandable and not to be short or efficient. While it still seems a little strange I am definitely looking forward to learn more Clojure. Again, you can download the source here.
Thanks for reading!
